本文共 1484 字,大约阅读时间需要 4 分钟。
1.堆内存溢出:
修改JVM参数:-Xms20m -Xmx20m -XX:+HeapDumpOnOutOfMemoryError

package cn.mxl.heap;import java.util.ArrayList;import java.util.List;public class OomHeap { public static void main(String[] args) { List 运行结果:

解决办法:
1.修改JVM参数,扩大堆内存 ;
2.通过Jconsole进行内存分析或者使用Eclipse Memory Analyzer,然后找到泄露的对象,进行处理;
这里要注意一下:内存泄露(memory leak)和内存溢出(memory overflow),笔者的理解是,第一个是在使用过程中因为不够,导致的异常,一个是线程申请的时候内存不够所抛出的异常,其中笔者个人觉得没有多大意义去区分它,我们分析方法和解决办法还是上面那两种;
2虚拟机栈和本地方法栈溢出
测试代码:
package cn.mxl.stack;public class JavaVMStack { private int test=1; public void stackLeak() { test++; stackLeak(); } public static void main(String[] args) { // TODO Auto-generated method stub JavaVMStack javaVMStack=new JavaVMStack(); try { javaVMStack.stackLeak(); } catch (Throwable e) { // TODO: handle exception System.out.println("test:"+javaVMStack.test); e.printStackTrace(); } }} 运行结果:
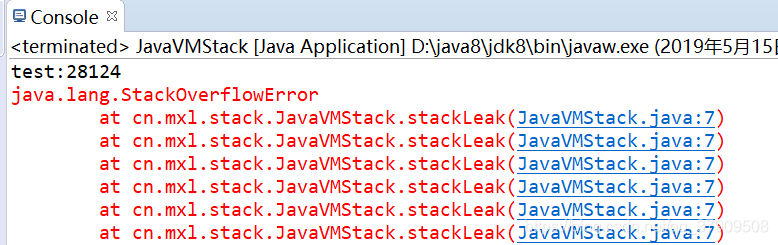
首先笔者还是想解释一下,这里为什么会出现栈溢出StackOverflowError的异常;首先那个int test笔者的目的只是观察被执行了几次这个方法,读者千万别以为和栈溢出有什么关系,栈溢出主要是由于栈帧太大导致的溢出,而我们的方法调用都保存在栈帧中,所以当我们不断的循环调用方法的时候,就会出现栈帧太大,导致栈溢出报Stack Overflow的异常.
栈的溢出可能会让我们想到递归,因为递归是很容易导致线程溢出的(还有多线程的情况下),那我们又该如何解决栈溢出呢?
1.传统的方式,减少不必要的线程数,或者增加虚拟机内存;
2.实际的方式,因为虚拟机内存是被heap和stack两个来平分的(这里不可能那些其他的占用虚拟机内存的区域),所以减少heap的内存,从而间接的增加stack的内存;
3.方法区和运行时常量池溢出
在之前jdk1.7的时候,通过String.intern()方法可以使得方法区溢出,但是如今String的常量池在1.8之后放到堆内存中,导致笔者也暂时没有想到哪个程序能够使得方法区溢出;
笔者只能提供一下一旦方法区溢出的解决办法:
1.排查,然后修改代码;
2.设置方法区内存值;
笔者在这里省略了一个本机直接内存溢出,想了解的可以去网上单独看看.
转载地址:http://zubhz.baihongyu.com/